Transformations of Functions

Transformation	f(x) Notation	Examples Using f(x) = x^3 as the original (parent) graph
Vertical Translation	f(x) + k Shifts k units up f(x) – k Shifts k units down	f(x) = x^3 + 3 shifts 3 units up f(x) = x^3 – 5 shifts 5 units down
Horizontal Translation	f(x – h) Shifts h units to the right f(x + h) Shirts h units to the left	f(x) = (x – 3)^3 shifts 3 units to the right f(x) = (x + 1)^3 shifts 1 unit to the left
Reflection	-f(x) “flips” graph over the x-axis f(-x) “flips” graph of the y-axis	f(x) = -x^3 reflects (“flips”) over the x-axis f(x) = (-x)^3 reflects over the y-axis
Vertical Stretch/Shrink	a·f(x) If a > 1 stretches If 0 < a < 1 shrinks	f(x) = 5x^3 stretch by factor of 5 f(x) = ½ x^3 shrink/compress by factor of ½
Horizontal Stretch/Shrink	f(ax) If a > 1 shrinks If 0 < a < 1 stretches	f(x) = (2x)^3 shrink/compress by factor of ½ f(x) = ( ¼ )^3 stretch by a factor of 4

You can combine all of these to form the following:

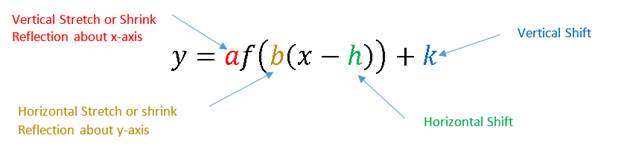
Compositions of Transformations (more than 1 transformation)

f(x – h) + k horizontal and vertical translations

Example f(x – 2) + 5 translate right 2 units and up 5 units

a·f(bx) Here the transformation would be a vertical stretch/compression by a and a horizontal stretch compression by b.

Example: Here the translation would be a vertical shrink by 1/3 and a horizontal stretch by 2.

So we multiply every y-coordinate by 1/3 and multiply every x-coordinate by 2.

a·f(x) + k Here we have a vertical stretch and a vertical translation.

However, there is some ambiguity here. What do you do first? Do you vertically translate, then vertically shift? OR do you shift then translate?

The ORDER OF OPERATIONS tells us to multiply/divide before we add or subtract.

So follow this order. Thus we multiply before we add.

Let’s take a look at this example:

3·f(x) + 4 for this transformation, we multiply every y-coordinate by 3 then add 4 while leaving the x-coordinates alone

f(ax - h) Here is another one that has some ambiguity to it.

This involves a horizontal stretch/shrink and a horizontal translation.

The answer is NOT to divide each x-coordinate by “a”, then add “h” as you might think. WHY??? The reason is that a problem presented like this is NOT written in standard form. We need to re-write this to be: f(a(x – c)) here c is the just h/a

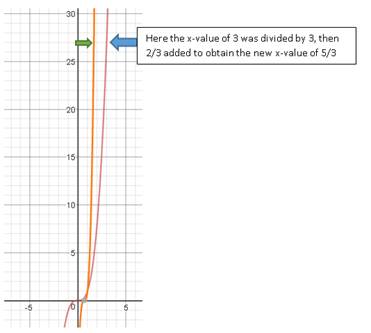
Here is an example:

f(3x – 2) we change this to standard form to be

Now take a look at the standard form. Here the correct shift would be to divide every x-coordinate by 3 then add 2/3.

Take a look at the following graphs of f(x) = x³, in red, and f(3x – 2), in orange.